数学霸凶残拟合 剑灵暴击率计算公式破解
2014-09-11 15:46来源：网络发布者：佚名新手卡|游戏下载|
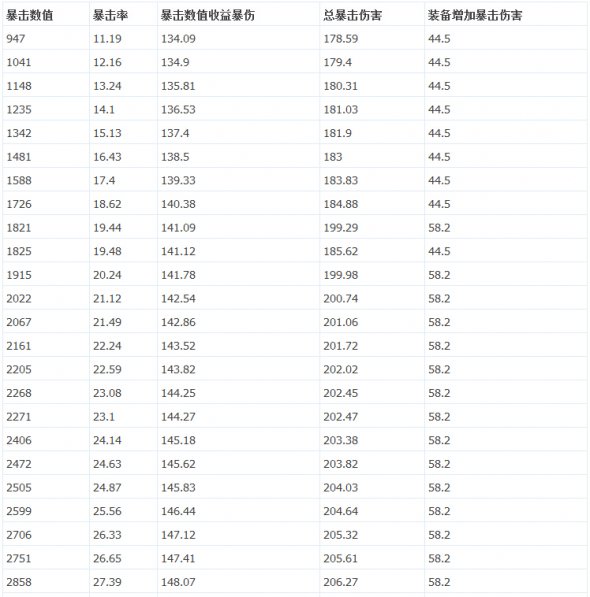
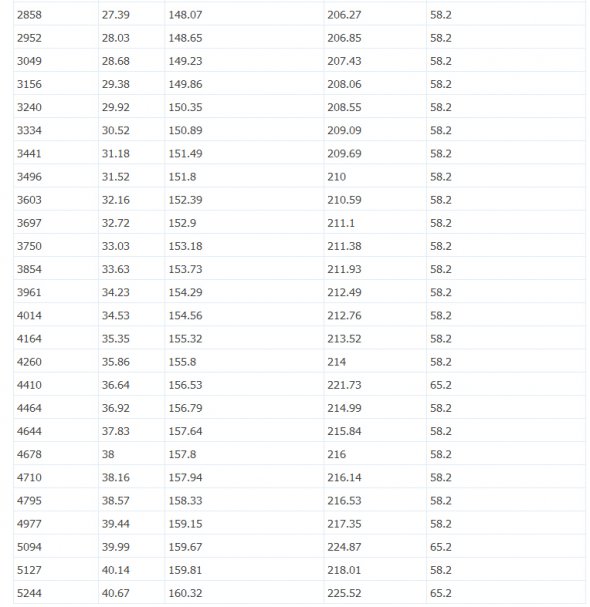
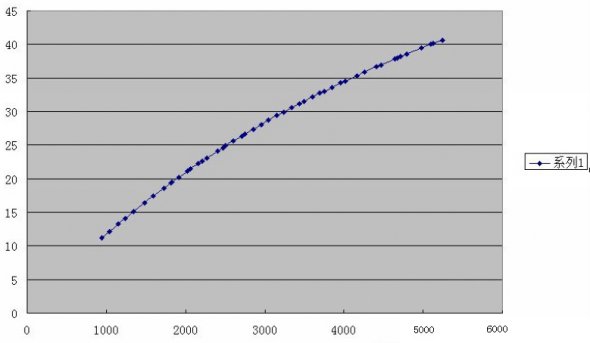
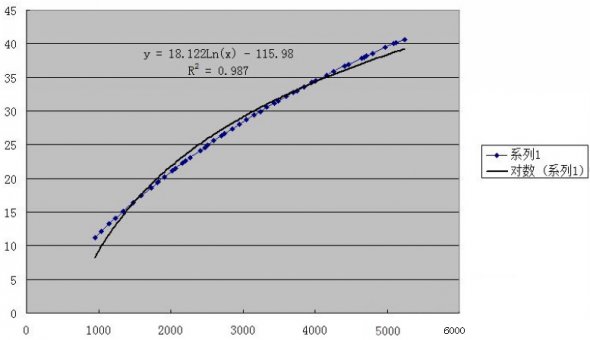
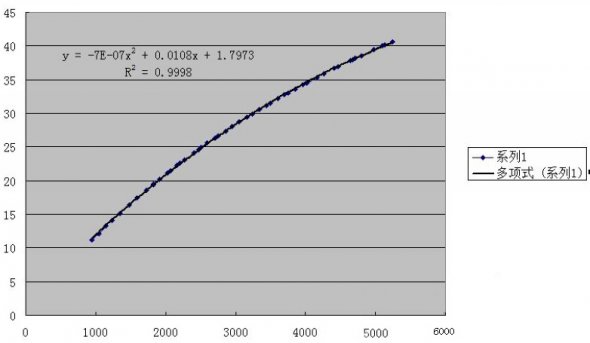
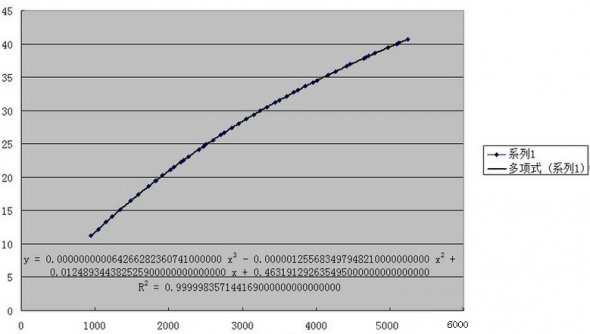
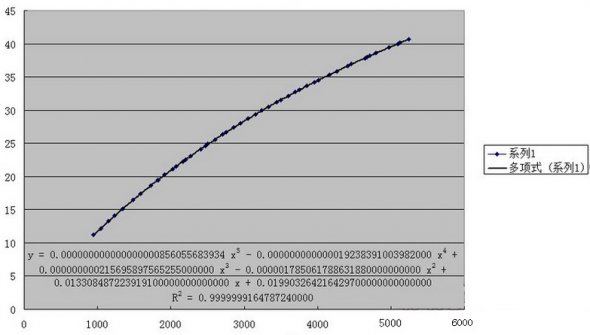
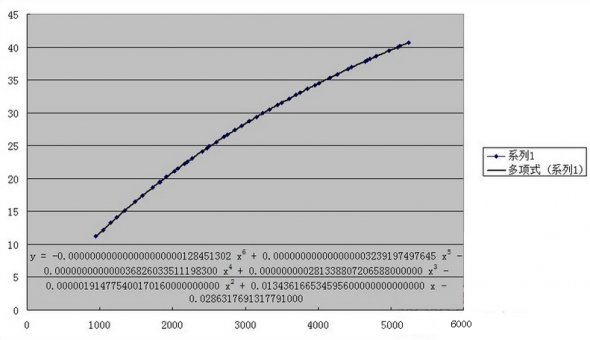
推荐阅读： 剑灵暴击率的计算公式： 稍微学过数学的都知道，剑灵的暴击率计算明显不是一个简单的函数可以满足的，于是这次使用了一个非常蛋疼的方法：线性回归方程。 不是简单的一次线性回归方程来推算，这样会显得太太太太太弱智了是不是。首先是一大组的数据统计： 取样：50级气功师  剑灵暴击函数  剑灵暴击函数 以上是我拼凑半天出来的属性，已经把土豪金放一遍避免打扰了。如果有兴趣拿笔算的孩子会发现，这特么真的不是人能总结的规律。 那么我们借助下工具，有请Excel登场。借助EXCEL来制作一个图表，我们可以大致得知：  剑灵暴击函数 乍看觉得像对数型函数，但是一拟合发现：  剑灵暴击函数 明显拟合不上啊，所以排除对数型和指数型。接下来可选类型就是多项式函数了，说实话EXCEL这功能确实强大，不过接下来才是杯具的开始，第二次拟合：  剑灵暴击函数 R^2=0.9998，醉了，不过也说明近似曲线是略符合原型函数的。 所以这一次的结果可以做参照，但是这只是第一次。接下来作死的开始。 第三次函数拟合：  剑灵暴击函数 继续继续，第四次函数拟合：  剑灵暴击函数 看来离真相不远了，第五次函数拟合：  剑灵暴击函数 最后一次，六次多项式函数：  剑灵暴击函数 看这里，但是别问我为什么R^2不愿意出来。 首先，暴击率的计算公式是一个高次多项式函数。 其次，EXCEL做近似曲线在多项式函数上最多实现6次函数的拟合，再高也帮不了你了。(但是手算的话，估计已经死了吧呵呵呵呵呵) 好了接下来是近似拟合的函数。 暴击率为y%，暴击数值为x 6次拟合后的结果为： y = -0.000000000000000000000128451302*x^6 + 0.000000000000000003239197497645*x^5 - 0.0000000000000368260335111983*x^4 + 0.000000000281338807206588^x*3 - 0.00000191477540017016^x*2 + 0.0134361665345956*x - 0.0286317691317791 看着略复杂对吧，但是我代入许多数值后，基本准确。 公式有偏差属正常现象，请大家理性看待。 如果有误或者有更好的算法可以私M我，我们可以一起讨论下，毕竟这个其实挺好玩的呢。 当然至于爆伤部分的公式我也就直接给出了，有疑问或错误请指点。 令暴击伤害为y%，暴击数值为x。公式如下： y = 0.00000000000000000000000579477*x^6 + 0.000000000000000000521669868168*x^5 - 0.0000000000000123483888760346*x^4 + 0.000000000136273693146027*x^3 - 0.00000120075658847925*x^2 + 0.0106524662294382*x + 124.973903190952 大致就是这样，欢迎有兴趣的一起来讨论下~
[编辑：Heyman]
|
本资讯及文章仅代表发表厂商及作者观点，不代表叶子猪本身观点！
